펜윅트리
필요없는 구간 지우기
- tree 배열은 오른쪽 끝 위치가 arr인 구간의 합이다.
- i, j 구간의 합은 j까지 누적합에서 i-1까지 누적합을 빼면 되는데, 만약 길이가 15일 때 8, 15 구간 합을 구한다고 하면 15구간합을 구하면 이미 8,15 구간합이 구해지기 때문에 필요없는 연산을 하는 것이다.

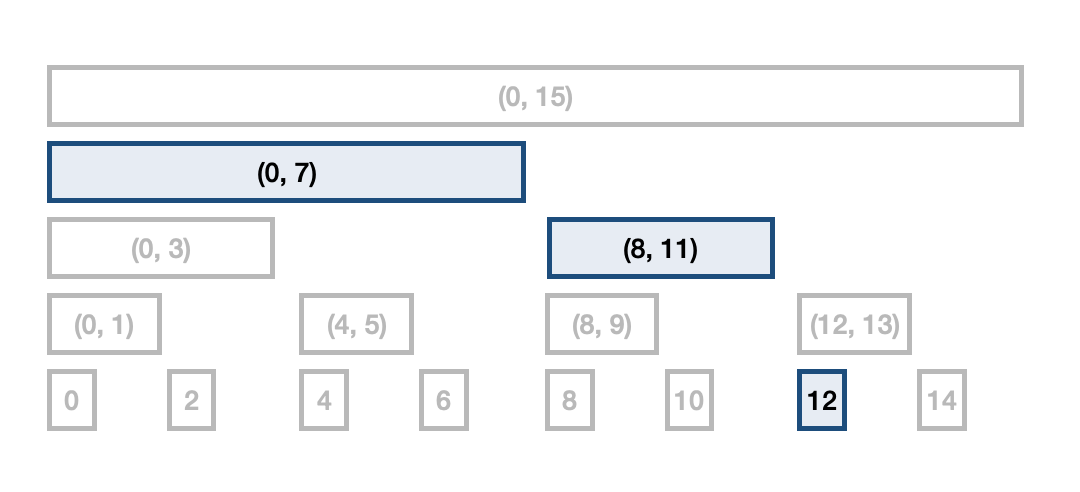
- 위의 이미지에서 필요없는 구간인 오른쪽 구간을 제거하고 왼쪽 구간만으로 구간합을 구할 수 있어서 왼쪽 구간만 냅두면 아래 이미지와 같게 된다.

- 여기서 12의 구간합을 구하고 싶으면 아래 이미지 처럼 0,7 8,11 12 3개의 구간합을 더 하면 된다.
이진수로 표현하기
- 펜윅트리는 각 숫자의 이진수 표현을 이용해 이 문제를 해결할 수 있다. 우선 이를 위해 배열 arr, tree의 첫 원소의 인덱스를 1로 바꿔준다. 모든 원소의 인덱스를 1씩 더해주면 된다.

이진수 표현으로 부분 합 구간 찾기
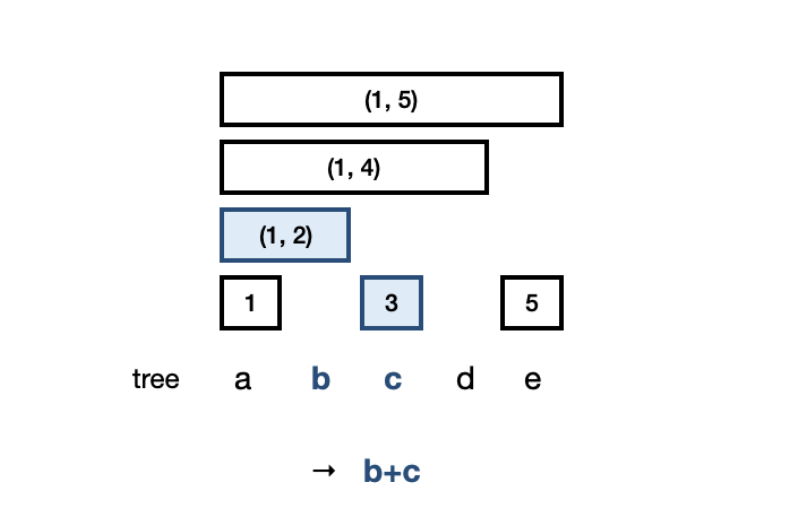
- 이제 부분 합을 구하기 위해 더해야 하는 구간들의 번호도 이들의 이진수 표현과 관계가 있다. 오른쪽 끝 위치의 이진수 표현에서 마지막 비트를 지우면 다음 구간을 쉽게 찾을 수 있다.
- 예를 들어서 7(0111)의 구간합은 `tree[7(0111)] + tree[6(0110)] + tree[4(0100)]` 처럼 이진수에서 마지막 비트를 0으로 바꾸면서 더해주면 된다.

이진수 표현으로 배열 값 변경하기
- 배열의 값을 변경하는 것은 해당 위치의 값에 숫자를 더하고 빼는 것으로 구현한다. 맨 오른쪽에 1인 비트를 스스로에게 더해주는 연산을 반복하여 해당 위치를 포함하는 구간들을 모두 만날 수 있다. 이 모든 구간에 값을 더해주면 된다.

일반 펜윅트리 구현
- 부분합 찾기, 값 변경 로직 모두 O(logn)의 시간복잡도를 가진다. 반복문이 수행될 때마다 트리의 한층을 올라가는데, 트리의 높이는 항상 O(logn)이기 때문이다.
- pos는 현재 값의 이진수 값
1. 배열 값 업데이트
- 배열 값을 변경하는 것은 해당 위치의 값에 숫자를 더하고 빼는 것으로 구현한다. 맨 오른쪽에 있는 1인 비트를 스스로에게 더해주는 연산을 반복하여 해당 위치를 포함하는 구간들을 모두 만날 수 있다.
pos += (pos&-pos);

2. 구간 합 구하기
- 이진수 표현에서 마지막 비트를 지우면서 다음 구간을 찾아가서 더해주면 된다. 오른쪽 끝 위치의 이진수 표현에서 마지막 비트를 지우면 다음 구간을 쉽게 찾을 수 있다.
pos &= (pos-1);
public class FenwickTree {
static int[] tree;
public FenwickTree(int size) {
tree = new int[size+1];
}
long sum(int pos){
long result = 0;
while(pos > 0){
result += tree[pos];
pos &= (pos-1);
}
return result;
}
void add(int pos, int val){
while(pos < tree.length){
tree[pos] += val;
pos += (pos & -pos);
}
}
}
구간 업데이트, 점 쿼리가 가능한 펜윅 트리
- 여기서는 구간 업데이트와 구간 합을 구할 수 있는 펜윅 트리도 설계할 수 있다. 배열 값을 인접한 값들의 차로 다음과 같이 설정한다.
b[1] = arr[1];
b[i] == arr[i] - arr[i-1];
1. 구간 업데이트 - (i,j) 에 k 더하기
- i부터 j까지 k를 더해줘야 한다.
- 예를 들어 3~4 에 6을 더해준다고 하면, 3이 포함되는 노드들에 +6을 해주고, 5가 포함되는 노드들에 -6을 더해주면 된다.

2. 점 쿼리 구하기 (Point Query)
- 현재 노드의 구간합은 노드의 이진수 표현에서 맨 뒤의 1을 없애면서 다 더하면 된다.

알고리즘 문제 추천
- 수열과 쿼리 21 (플래티넘 4)
참고 자료
https://loosie.tistory.com/647











댓글